2.8.9 Asteroiden-Stabilität
Man entdeckt heutzutage Asteroiden (Meldung Januar 2026: „2025 MN45“, 710 m groß, 1,88 Minuten/Umdrehung!), deren Größe und Stabilität nicht zueinander zu passen scheinen: Sie sollten eigentlich zerrissen werden, falls sie aus gravitativ zusammengehaltenem Schotter bestünden. Also sind sie fest! (Und: Wo kommen sie dann her, wenn sie nicht im Gürtel-Schotter zusammengefunden haben?)
Dazu will ich versuchen, erst einmal die Parameter zu ermitteln, die auf ihre mechanisch-gravitative Stabilität Einfluss haben. Dazu berechnen wir alle wirkenden Kräfte und setzen sie ins Verhältnis zur Zugfestigkeit eines angenommenen homogenen und isotropen Stoffes einer bestimmten Dichte.
Welche Kräfte sind das, die wir berücksichtigen müssen?
a) interne Schwerkraft des Asteroiden: hält ihn zusammen
b) eigene Rotation: zieht ihn durch Fliehkraft auseinender
c) externe Schwerkraft (z.B. durch Zentralkörper oder Nachbarn): zieht ihn statisch durch deren Gradienten auseinander (wie auch Gezeiten gebildet werden)
d) Trajektorie um externes Zentrum: zieht ihn dynamisch durch Fliehkraft-Gradienten und GG-Geschwindigkeits-Gradienten auseinander
Welche Geometrie wäre extrem anfällig oder extrem stabil?
Man dürfte nach einigem Überlegen darauf kommen, dass eine Kugel relativ stabil und ein Stab relativ instabil sein sollten.
Wo soll das Zerreißen stattfinden?
Man sollte also auch noch unterscheiden, ob der Körper zentral zerrissen wird (also in zwei gleich große Teile) oder ob am entferntesten Punkt vom Schwerpunkt (also am Rand) ein Teil losgerissen wird. Gibt es also eine Wahrscheinlichkeits-Funktion längs des Körpers für das Zerreißen?
Die resultierende Kraft muss dann in jedem Fall, den wir betrachten wollen, mit der Kraft, die sich aus Zugfestigkeit und Querschnittsfläche ergibt, verglichen werden.
Was immer geht: Diskretisierung und numerische Integration. Die Frage ist wie immer in der Physik, ob man sich durch Symmetrie-Überlegung die Arbeit vereinfachen kann.
A) Vermutlich stabilster Fall: Asteroid als homogene Kugel
a) Interne Schwerkraft
Berechnen wir zuerst die interne Gravitation. Wir wollen die Gesamt-Kraft berechnen, die senkrecht zu einer Äquatorebene wirkt, um das Zerreißen inder Mitte zu bestimmen. Dazu können wir alle senkrecht zu dieser Ebene wirkenden Kraftkomponenten addieren (Gegenkräfte NICHT addieren, die sind axiomatisch gleich groß; andere Komponenten als die senkrechten heben sich symmetrisch auf!).
Wir wissen aus früheren Überlegungen, dass
erstens eine homogene Kugel im äußeren Schwerefeld durch ihren Schwerpunkt ersetzbar ist und
zweitens das Feld innerhalb einer homogenen Kugelschale verschwindet
woraus folgt, dass innerhalb einer homogenen Kugel ein konstanter Kraftgradient F‘ entlang des Radius r existiert.
Die radiale Element-Kraft dF ist im Zentrum Null und an der Oberfläche dF = R*F‘.
Daraus folgt für die Kraft eines Volumenelements senkrecht zur Äquatorialebene mit Zenitwinkel theta und Mittelpunktabstand r:
dFz = r*F’*cos(theta) * dV/V (V=Halbkugel-Volumen)
Diese Kraft ist für alle dV auf einem äquatorparallelen Kreisring (alle Azimutwinkel phi von 0 bis 2*pi) der Parameter r und theta gleich und kann also zusammengefasst werden zu
dFz(Ring) = 2*pi*r*F’*cos(theta) *dV(Ring)/V
Die Integration über r und theta ergibt dann die Kraft zwischen den beiden Halbkugeln, wenn man dV(Ring) ebenfalls entsprechend variabel gestaltet.
Man kann atatt der ringförmigen auch näherungsweise mit identischen würfelförmigen dV in kartesischen Koordinaten arbeiten und die Kugeloberfläche stets als Grenze berücksichtigen. Dann könnte man „Stäbe“ oder „Scheiben“ aus den dV bilden und diese einfacher integrieren oder eben eine dreifache Summation innerhalb des Randes (hier: Halbkugeloberfläche) ausführen.
Für ein Volumenelement dV=dx*dy*dz gilt dann mit
cos(theta) = z/r
und
F(r) = dm*M(innen)*G/r² = rho*dm*4/3*pi*r³*G/r² = 4/3*pi*rho*G*dm*r
(oder, um unabhängig von der differentiellen Masse dm zu sein, als Beschjleunigung formuliert: a(r) = F(r)/dm = 4/3*pi*rho*G*r)
Der Kraftgradient ist dann konstant:
F‘ = 4/3*pi*rho*G*dm = const
Die z-Komponente der Kraft ist dann nur von z abhängig, und zwar linear:
dFz = r*F’*cos(theta)*dV/V = z*F’*dV/V
Darf man hier vermuten, dass die Summation über die gesamte Halbkugel ein Ergebnis bringt, das mit der Kraft einer im Schwerpunkt der Halbkugel (übrigens bei z= 3/8*R) konzentrierten Masse der Halbkugel identisch ist?
Ja, das darf man, weil der Beitrag der zur Äquatorebene parallelen Kreisscheiben wie beim Schwerpunkt nur von z selbst abhängt!
F = F’*Integral(A(z)*z*dz)(0 bis R) = F’*pi*Integral((R²-z²)*z*dz)(0 bis R)
F = F’*pi*Integral((R²z-z³)dz(0 bis R) = F’*pi*(R²z²/2-z^4/4)(0 bis R)
F = F’*pi*((R^4/2-R^4/4) = pi/4*F’*R^4 = F‘ * 2*pi/3*R³ * 3/8*R
F = F‘ * V(Halbkugel) * 3/8*R
(Dimensionen korrigieren!!)
Trotzdem sollte man eine numerische Integration einrichten, um das Ganze auch auf dreiachsige Ellipsoide erweitern zu können!
(Interessant: Das eine extreme Ellipsoid wäre der dünne Stab, bei dem man auf Zmax/2 käme, oder die dünne Kreisscheibe mit ebenfalls Zmax/2. Die Kugel ist unter diesem gravitativen Aspekt wahrscheinlich die größte Abweichung (relatives Minimum bzgl. zmax 25% geringer) vom allgemeinen Ellipsoid!)
b) Fliehkraft durch Eigenrotation
Die Formabhängigkeit dieser Kraft wird uns nun bei der Eigenrotation wegen der Radiusabhängigkeit bzgl. der Rotationsachse (die in der Schnittebene der beiden Form-Hälften liegen sollte, weil sie durch den Schwerpunkt gehen muss) wiederum interessieren, da kann wiederum der Stab – je nach Achse – am ungünstigsten sein!
Aber zuerst wieder die Kugel: Hier haben wir bei einer gegebenen Winkelgeschwindigkeit eine Proportionalität von Fliehkraft in achsradialer Richtung und Achsabstand. Es wird wiederum die Summe der Komponenten senkrecht zur Äquatorialebene gesucht, zu der diesmal aber eben diese Achse gehört.
Hier spielt also der Achsabstand statt des Mittelpunktabstands für die Kraft auf das Volumenelement dV eine Rolle, von der wir wieder lediglich die Komponente senkrecht zur Schnittebene benötigen (alle anderen heben sich aus Symmetriegründen auch beim 3-achsigen Ellipsoid gegenseitig auf).
Statt des obigenKugelradius
r=Wu(x²+y²+z²)
haben wir jetzt einen (Rotations-Achse in der x-Achse) Zylinderradius
r=Wu(y²+z²)
und die senkrechte Komponente statt des obigen Schwerkraft-Ansatzes
dFsz = r*F’*cos(theta)*dV/V = z*F’*dV/V
nun den Fliehkraft-Ansatz
dFfz = w²*r*cos(gamma)*dV/V = z*w²*dV/V
mit cos(gamma) = z/r und w als Winkelgeschwindigkeit um die x-Achse
Formal bedeutet das, in die Ungleichung für das Stabilitätskriterium zwischen Schwerkraft Fsz und Fliehkraft FFz sowie maximaler Zugkraft Fzzmax
Ffz-Fsz < Fzzmax
die richtigen geometrischen und kinematischen (extensiven) und materialtypischen (intensiven) Größen einzusetzen und möglichst zu vereinfachen, wobei von vornherein klar geworden ist, dass der Schwerkraftgradient F‘ (als Funktion der Dichte) und die Winkelgeschwindigkeit w (z.B. als Funktion des Drehimpulses) in zweiter Potenz als Gegenspieler auftreten.
Für einen aus Schotter bestehenden Asteroiden fällt die Zugfestigkeit weg und die Gleichung reduziert sich auf
Fsz > Ffz
dm*4/3*pi*rho*G*R > dm*w²*R
und also
4/3*pi*rho*G > w²
Das ist sehr interessant, denn es bedeutet, dass ein kugeliger schotteriger Himmelskörper eine radiusunabhängige Maximaldrehzahl hat, unter der er nicht mittig auseinanderfliegt.
Setzt man für rho=8000 kg/m³ (Nickel-Eisen) und für G=6,67 Nm²/kg² ein, erhält man 0,8 Umdrehungen pro Stunde und für rho=1000 kg/m³ (Eis) 0,3 Umdrehungen pro Stunde. (Gestein läge dazwischen) Da der Schotter nicht wirklich dicht gepackt sein wird, muss man mit um etwa 30% kleineren Werten rechnen, also etwa 0,6 bzw. 0,2 Umdrehungen pro Stunde.
(Wir erinnern uns an etwa solche „Sprungzeiten“ im Stundenbereich der abgeprallten langsam landenden Sonde auf einem Asteroiden, die nicht einmal als Teil einer Kugeloberfläche anzusehen war, sondern wahrscheinlich an der Längsseite des Asteroiden landete, wo die resultierende Schwerebeschleunigung zusätzlich noch reduziert sein musste…)
Lassen wir zu, dass der Asteroid (wie der extrasolare Oumuamua von 2017 als langer 10:1-Stab in etwa 7 bis 8 Stunden oder erst recht der 2025 MN45 vom Januar 2026 in sage und schreibe 1,9 Minuten (710m Durchmesser)) tatsächlich deutlich schneller rotiert, so muss eine Zugfestigkeit vorhanden sein.
Setzen wir diese als sigma in die Ungleichung ein, erhalten wir eine wie folgt dimensionierte Kraft über die äquatoriale Schnittfläche:
Fzz = sigma*Fläche = sigma * pi * R²
Formen wir das über die Masse in eine Beschleunigung um und teilen durch den Radius, kommen wir auf die gleiche Dimension wie in der obigen Gleichung und erhalten
Fzz/(MHalbkugel*R) = sigma*pi*R²/(2/3*pi*rho*R³*R) = 2/3*rho/R²
Erstaunlicherweise wird die Gegenwirkung der Zugfestigkeit als „relative Beschleunigung“ (1/s²) mit größer werdender Kugel überproportional kleiner. Die Masse wächst eben mit der dritten Potenz des Radius und die Zugkraft nur mit der zweiten! In einem Asteroiden-Gürtel sind deshalb große oder erst recht längliche Objekte bei ständigen Begegnungen, die Drehimpulse übertragen können, benachteiligt.
Ein Zahlenbeispiel soll das veranschaulichen:
(kommt noch)
B) Vermutlich instabilster Fall: Stabförmiger Asteroid
a) Interne Schwerkraft
Setzen wir den Stab aus einer geraden Anzahl von identischen Würfeln zusammen, kommen wir auf eine interessante Funktion für die Schwerkraft jedes Würfels (damit ist die Kraft gemeint, die ihn zum Zentrum des Stabes zieht).
Für den äußeren Würfel ergibt sich die Summe aller einzelnen Schwerkräfte, also bis auf eine Konstante die Summe der reziproken Quadrate der Abstände, welche wir als natürliche Zahlen (ganzzahlige Vielfache der Würfel-Kanten-Länge) behandeln können:
Diese Summe hat den Grenzwert pi²/6=1,645… und ähnelt entfernt der Arkustangensfunktion (wer denkt hier schon an Balken-Galaxien??):
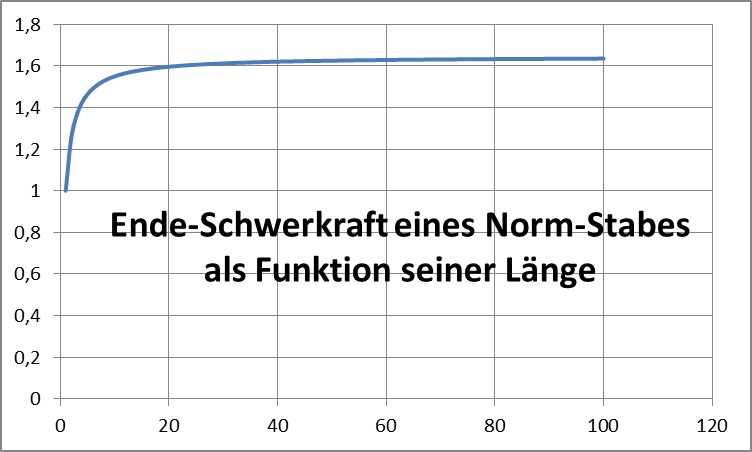
Will man die Werte für die inneren Würfel berechnen, so muss man alle vorhandenen symmetrisch entfernten Nachbarn weglassen, da sich ihre Grafitationskräfte aufheben.
Es ergibt sich ein interessantes Schema und eine noch interessantere Zusammenfassung:
Der erste Würfel neben der Mitte (i=1) hat als resultierende Kraft nur diejenige des äußersten (i=n) Gegenübers (Abstände werden von dern Würfelmitten aus gemessen).
Der zweite Würfel neben der Mitte (i=2) hat als reslultierende Kraft nur die der drei äußeren Gegenüber und so weiter und so fort…
Bis auf Konstanten ergibt sich also für jeden Würfel einzeln:
F(1) = 1/n²
F(2) = 1/n² + 1/(n+1)² + 1/(n-1)²
F(3) = 1/n² + 1/(n+1)² + 1/(n-1)² + 1/(n+2)² + 1/(n-2)²
F(n) = Summe(1/i²)(i von 1 bis 2n-1)
Baut man nun die Folge der Gesamtkraft für jede Würfelberührung von außen nach innen auf, ergibt sich das Schema am Beispiel für n=5:
F(5) = 1/1² + 1/2² + 1/3² + 1/4² + 1/5² + 1/6² + 1/7² + 1/8² +1/9²
F(4) = 1/2² + 1/3² + 1/4² + 1/5² + 1/6² + 1/7² + 1/8²
F(5)+F(4) = 1/1²+ 2/2² + 2/3² + 2/4² + 2/5² + 2/6² + 2/7² + 2/8² + 1/9²
F(3) = 1/3² + 1/4² + 1/5² + 1/6² + 1/7²
F(5 bis 3) = 1/1²+ 2/2² + 3/3² + 3/4² + 3/5² + 3/6² + 3/7² + 2/8² + 1/9²
F(2) 1/4² + 1/5² + 1/6²
F(5 bis 2) = 1/1²+ 2/2² + 3/3² + 4/4² + 4/5² + 4/6² + 3/7² + 2/8² + 1/9²
F(1) = 1/5²
F(alle: 5 bis 1) = 1/1²+ 2/2² + 3/3² + 4/4² + 5/5² + 4/6² + 3/7² + 2/8² + 1/9²
oder verallgemeinert
F(alle) = 1/n + Summe(1/i+(n-i)/(n+i)²) für (i=1 bis (n-1))
als Gesamt-Schwerkraft auf die zentrale Schnittfläche des Stabes. Ihre grafische Darstellung ergibt erstaunlicherweise folgendes:
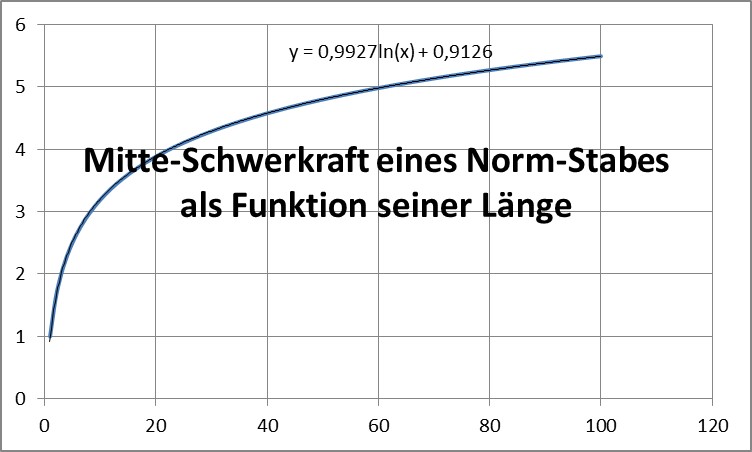
Die Funktion lässt sich nähern durch F(n) = ln(n) + 1 und ist damit der Eulerschen Näherungsformel für die Summe der reziproken natürlichen Zahlen (ln(n)+0,577) sehr nahe. Das heißt, dass die fallenden Zusatzterme in der zweiten „Hälfte“ der Summe einen zunehmend vernachlässigbaren Wert ergeben, da ihre Summe sehr schwach steigt und etwa die Differenz zur Eulerschen Zahl 0,577 ergibt:
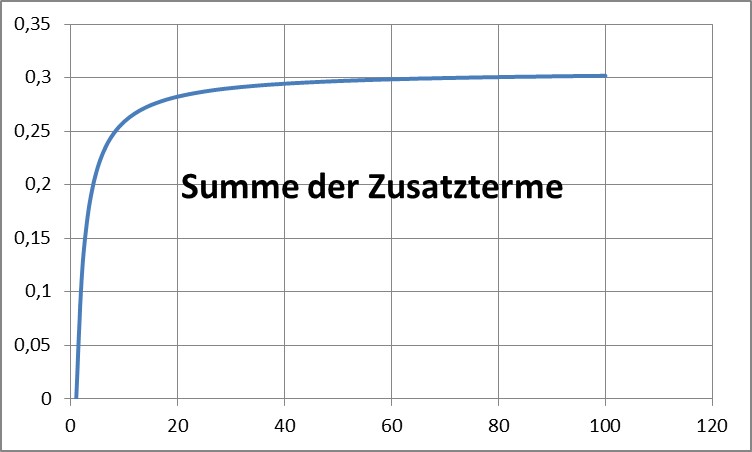
b) Fliehkraft
Hier haben wir es mit einem einfachen Zusammenhang zu tun, denn
Ff(n) = m*w²*n
als Kraft für den n-ten Würfel von der Mitte lässt sich leicht für den halben Stab (ganzer Stab mit 2n Würfeln) summieren:
Ff(alle n) = m*w²*(n²/2+n/2)
Damit steht der negativ gekrümmten Gravitationskraft-Funktion eine drehzahlabhängige positiv gekrümmte Fliehkraft-Funktion gegenüber, was dem Bauchgefühl für die Instabilität langer Stäbe gut tut.
Interessant ist dann der Vergleich der einzelnen Würfel-Berührungsflächen: Welche ist die der größten Instabilität bezüglich Schwer- und Fliehkraft? Wo also reißt der Stab zuerst?
Wir tragen also die Gesamt-Schwerkraft (blau) und die entgegen wirkende Gesamt-Fliehkraft (rot) ortsabhängig längs eines gegebenen Stabes auf (wir haben einen Stab der Länge 25 gewählt):
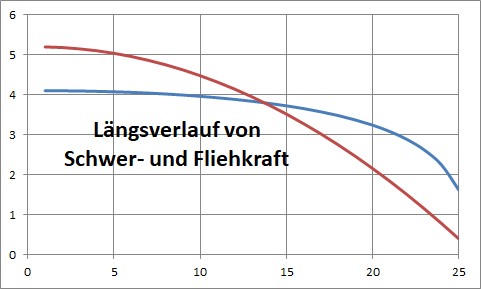
Die tatsächlichen Zahlenwerte sind dann von den physikalischen Parametern abhängig und können an einem Beispiel demonstriert werden:
(kommt)
c) externe Schwerkraft
Von der Beschäftigung mit den Gezeitenwirkungen durch Sonne und Mond wissen wir, das allein der Gradient des Schwerefeldes wichtig ist und nicht die Sxchwerkraft selbst: Obwohl die Sonne eine größere Kraft auf die Erde ausübt als der Mond, ist dessen Kraftgradient größer, weil seine größere Nähe überwiegt. (Auf dem Mond ist es ebenso, obwohl auch dort die Sonne die größere Kraft ausübt. Siehe dort!)
Setzen wir also einen genähert konstanten Gradienten an und justieren wir diese Korrektur-Kraft im Schwerpunkt auf Null, so erhalten wir eine lineare Zusatzfunktion zur Fliehkraft, die diese nach oben kippt.
d) Kohäsion
Die Kohäsion (Reißfestigkeit) können wir bei einem homogenen Stab konstant ansetzen. Sie verschiebt also die Gravitationskurve nach oben.
Die Gesamtdarstellung ergibt dann folgendes Bild:
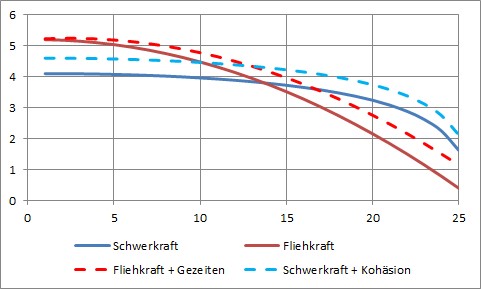
Die Kohäsion kann natürlich noch viel stärker sein, so wie auch die anderen Parameter physikalisch anders gestaltet sein können, sodass es gar keine Kreuzungen der roten und blauen Funktionen im gewählten Wertebereich geben muss.
Eines aber ist sicher: Sowie der Stab eine bestimmte drehzahlabhängige Mindestlänge erreicht, wird er zerreißen müssen.
–
Wir verstehen nun, dass die Saturnringe stabile Zustände sind, da sich neubildende und zerfallende Agglomerate die Waage halten.
Unter Beachtung relativistischer Effekte darf man vermuten, dass das auch für Galaxien-Strukturen gelten kann. Da aber die Anzahl ihrer Rotationen seit ihrer Bildung oft sehr gering ist, ist auch der Begriff „Stabilität“ an sich fragwürdig.
Kommentar abgeben