Primzahl-Spielchen
Wozu braucht man denn, bitteschön, PRIMZAHLEN ??
Erinnern wir uns an die Grundrechenarten:
Sie sind unverdächtig, menschliche Künsteleien zu sein, wenn sie in der Natur und auch beim Mengenverständnis der Tiere auftauchen.
Ausgangspunkt sind immer abzählbare (und in diesem Zusammenhang unteilbare) Objekte. Die kann man sammeln (zum Beispiel ernten!) und dann die Mengen vergleichen. Grob geht das auf den ersten Blick, für genauere Auskünfte über ähnlich erscheinenden Mengen hilft das Abzählen. (Blöde erscheinende Definition: Man spricht von „abzählbaren“ Mengen, sofern sie kleiner als Unendlich sind, also zum Beispiel die Anzahl der Atome unserer Erde sowie sämtliche Permutationen ihrer Anordnung…)
Für uns soll hier „abzählbar“ bedeuten, dass wie jedes der Objekte einer Menge als solches einzeln erkennen und ihm eine Zähl-Zahl zuordnen können.
Wollen wir nun die Ernte aufteilen, kann sich ein Problem ergeben, wenn wir fair sein wollen: Es kann vorkommen, dass nicht alle die gleiche Anzahl von Objekten bekommen können, weil die gesamte Menge nicht ohne Rest durch die Anzahl der Empfänger teilbar ist, wenn man mal von dem zufällig (oder „willkürlich“) erscheinenden Sonderfall absieht, dass die Menge der Objekte der Menge der Empfänger entspricht. (Der andere Sonderfall, dass es keinen weiteren Empfänger gibt, ich als Nummer 1 also alles behalten kann, ist ebenfalls uninteressant.)
Wenn wir als Sonderfall einer Objekt-Menge betrachten wollen, dass bei jeder beliebigen gleichwertigen Aufteilung unter der (variabel gedachten!) Empfänger-Menge ein Rest bleibt, so können wir diesen Fall „Primzahl“ nennen.
Theoretische (fast philosophische!) Frage: Sind dann alle Primzahlen von gleichem „Rang der Besonderheit“?
Nehmen wir die 2:
Es gibt keine ganze Zahl außer der 2 und der 1, durch die man die 2 teilen könnte, so dass die allgemeine Primzahldefinition von oben, dass es keine Zahl außer den beiden Sonderfällen „1 Empfänger“ oder „Empfängerzahl gleich Objektzahl“ gibt, durch die sie ohne Rest teilbar ist, obsolet wird.
Nehmen wir die 3:
Ist eine Zahl außer durch 1 und durch sich selbst ohne Rest teilbar, so muss es mindestens zwei Faktoren geben, deren geometrisches Mittel der n-ten Wurzel der Zahl entspricht, wenn n die Anzahl der Faktoren ist. Da die 2. Wurzel von 3 kleiner als 2 ist, müsste einer der (als ganzzahlig geforderten!) Faktoren 1 sein, was ein Widerspruch in sich ist.
Im strengen Sinne können wir also die 2 und die 3 aus der Menge der Primzahlen ausschließen. Die kleinste wäre somit die 7, denn auch bei der 5 könnten lediglich die 2 und die 3 (die wir ja beide schon kritisch sehen!) als Faktoren auftreten, deren Produkt aber schon 6 ergibt, welches die kleinste Zahl als Produkt aus zwei verschiedenen ganzen Zahlen je größer 1 und je ungleich jedem Faktor ist. Lassen wir zwei gleiche Zehlen zu, so wäre 2 x 2 = 4 und also die 5 die kleinste Primzahl.
Es ergibt sich eine interessante Splittung der Definition:
Primzahl ist nicht gleich kleinstmöglicher Teiler.
Damit wird der Begriff „Primfaktor“ vom Begriff „Primzahl“ getrennt, was zwar blödsinnig klingt, aber unumgänglich ist.
12=2x2x3 ist dann immer noch eine gültige Zerlegung!
Um diesem Dilemma auszuweichen, belässt man die 2, 3 und 5 unter den „Primzahlen“ und somit auch Primfaktoren. Man sollte sich der Unsauberkeit aber bewusst sein, wenn man damit zu höheren Operationen übergehen will. Eine Splittung wäre durch einen neuen Begriff wie Basiszahl („base number“) möglich, wie er von Professor Klaus Hennig benutzt wird:
(https://www.researchgate.net/publication/394528773_About_base_numbers_and_real_prime_numbers_in_the_system_of_natural_numbers)
Die Besonderheit der „37“
In unserem Physik-Studium hatten wir in Analytischer Geometrie einen Dozenten an der TU Dresden (Prof. Gerhard Geise), dessen Lieblingszahl die 37 war. Ihm zu Ehren ziert diese Zahl heute noch unser Auto-Kennzeichen…
Sie ist besonders: Sie ist eine Primzahl mit der Quersumme 10, deren Spiegelung (73) ebenfalls eine Primzahl ist. Davon gibt es bis zur 100 nur dieses Pärchen. Bis zur 1.000 kommt keine weiteres hinzu. Bis zur 10.000 kommen nur zwei weitere Pärchen (1.009/9.001 und 1.153/3.511) hinzu. Erst dann wird es – in logarithmisch betrachteten Intervallen – etwas „fülliger“:
9 neue bis zur 100.000
20 neue bis zur 1.000.000
35 neue bis zur 10.000.000
64 neue bis zur 100.000.000
Die Primzahleigenschaft ist eine Mengen-Eigenschaft und damit Zahlensystem-unabhängig (auch bei Oktal-, Nonal- oder Hexadezimalzahlen sind die gleichen Mengen prim oder nicht.)
Schreiben wir die 37 im Nonalsystem als 41(9), so ist ihre Spiegelung 14(9) und somit 13 und auch wieder prim!!
Schreiben wir die 37 im Undezimalsystem, ergibt sich 34(11), so ist die Spiegelung 43(11)=47 eine Primzahl.
Schreiben wir die 37 im Heptalsystem als 52(7), so ist die Spiegelung 25(7)=19 eine Primzahl.
Schreiben wir die 37 im Pentalsystem als 122(5), so ist die Spiegelung 221(5)=61 eine Primzahl.
Schreiben wir die 37 im Trialsystem als 1101(3), so ist die Spiegelung 1011(3)=31 eine Primzahl.
Wer will das weiter erforschen???
Und setzen wir eine neue Reihe an, indem wir die geforderte Quersumme der Primzahl-Pärchen variieren, ergibt sich eine interessante Verteilungskurve für die Quersummen von 4 bis 44 (bis zur Grenze von 99.999):
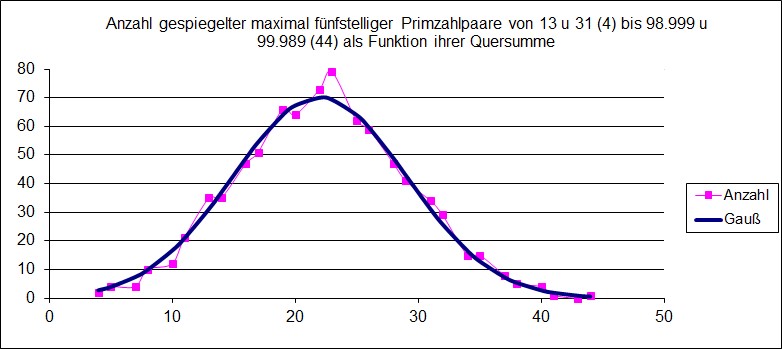
Die Gaußkurva habe ich händisch durch Parameter-Variation angepasst… Sowas machen nur Rentner mit Langeweile… (Wenn die geforderte Quersumme das Produkt von Stellenzahl und 9 erreicht, wird es natürlich „Unfug“, deshalb die Begrenzung hier auf 44.)
Freue mich auf Kommentare!!
Kommentar abgeben